Dr. A. Lobel
Royal Observatory of Belgium

Stellar Atmospheric Stability Theory

Research

The atmospheres of cool massive supergiants are unstable, which causes pulsation-variability, strongly developed large-scale atmospheric motion fields, excessive mass-loss, and extended circumstellar envelopes. Although the kappa- and gamma-mechanisms have been identified as the main cause for driving pulsations of the less luminous high-gravity atmospheres of Cepheids, little is known about the efficiency of these effects for the much more extended and tenuous atmospheres of cool massive supergiants. In detailed calculations of the first generalized adiabatic index Gamma_1, I found that this quantity assumes very small values, below 4/3, in low-gravity model atmospheres with 5000 K <= Teff <= 8000 K, primarily due to the partial thermal ionization of hydrogen.

It has been suggested that enhanced mass-loss due to ionization-induced dynamic instability of the outer envelope of luminous supergiants which evolve redwards, would terminate their redward movement, and provide a possible explanation for an observational lack of yellow and red supergiants with log(L*/L_sun) >= 6.0. However, the major problem for evaluating supergiant dynamic (in)stability, based on detailed calculations of Gamma_1, is the breakdown of Local Thermodynamic Equilibrium (LTE) conditions in these very extended atmospheres. The importance of non-LTE ionization- and excitation-conditions is evident from modeling the spectra of these stars, which are formed in conditions of very small gravity acceleration. The local ionization equilibrium is strongly determined by the stellar radiation field, which determines important thermodynamic quantities such as the heat capacities, and the related mechanical compressibility of these atmospheres.

I have developed a self-consistent thermodynamic formalism that accounts for departures from LTE for the calculation of Gamma_1. This goal is accomplished by introducing the temperature of the radiation field as an independent state variable that can differ from the local kinetic gas temperature. The formalism accounts for departure from thermal ionization equilibrium by an incident and diluted stellar radiation field in the Eddington approximation. Analytic expressions for the computation of Gamma_1 and the heat capacities in mixtures of monatomic gas, interacting with radiation are derived. The departures from LTE conditions due to the interaction of matter and radiation are included by evaluating the fundamental thermodynamic quantities accordingly.


Results

From a numerical application of the new formalism to a grid of supergiant model atmospheres (with solar elemental abundance values) and 4000 K <= Teff <= 20,000 K, I find that the local values of Gamma_1 become very small, below 4/3, over a large fraction of the atmosphere for models with Teff between 7000 K and 8000 K (Fig. 1). This results from the incident radiation field with a temperature of the order of the stellar effective temperature, which primarily causes partial photo-ionization of hydrogen. These regions displace deeper down the atmosphere with raising Teff, whereas the thermal partial ionization regions, at the base of the atmosphere, displace outwards. This combined effect causes the deep minimum in the local values of Gamma_1 to occur for these cool star atmospheres. Around these effective temperatures, partial non-LTE ionization causes very high atmospheric compressibilities, by which Gamma_1 can even decrease to below unity.

Numerical evaluations of Ledoux' stability integral < Gamma_1 > down into the stellar envelope demonstrate that < Gamma_1 > exceeds 4/3 in supergiant models for which a hydrostatically stable solution can be computed. Towards smaller gravity accelerations < Gamma_1 > decreases, and models become unstable with < Gamma_1 > < 4/3 at the base of the envelope. Stable models with smaller atmospheric gravity assume smaller < Gamma_1 >-values, and Ledoux' stability integral verifies that models of higher Teff destabilize at increasingly larger gravity-values due to the enhancement of radiation pressure.

Most importantly, the theory reveals that for stable supergiant models with 6500 K <= Teff <= 7500 K, < Gamma_1 > assumes minimum values, below 4/3, over a very large fraction of the atmosphere down to its base. Around Teff=6500 K this minimum occurs practically independently of the atmospheric gravity acceleration. For a given Teff, in atmospheres of increasingly smaller gravity, < Gamma_1 > assumes small values in layers of increasingly lower density due to enhanced partial ionization with the dilution of the radiation field. This corresponds to dynamically destabilizing regions, extending over an increasingly larger geometric fraction in the upper atmospheres of more massive cool supergiants.

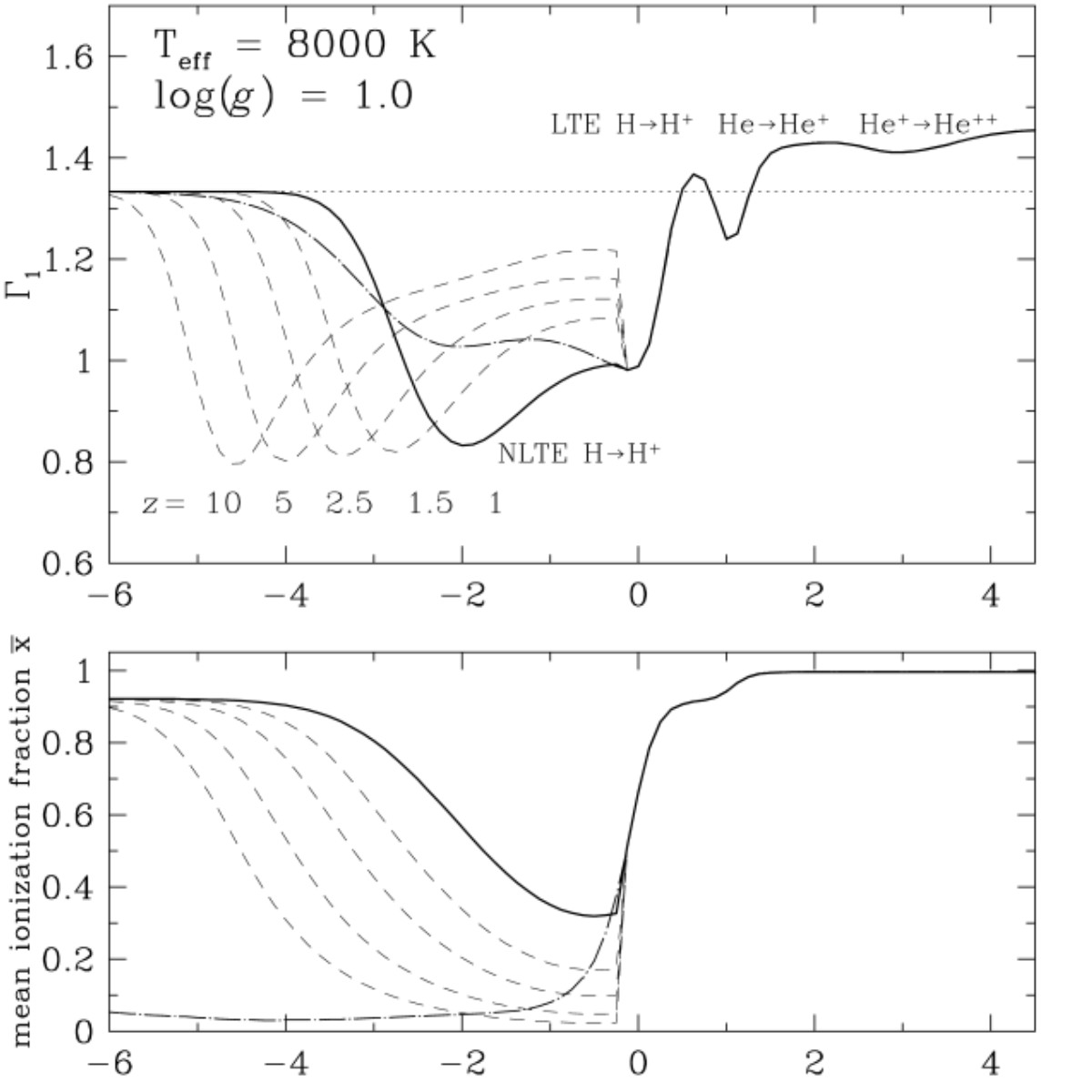
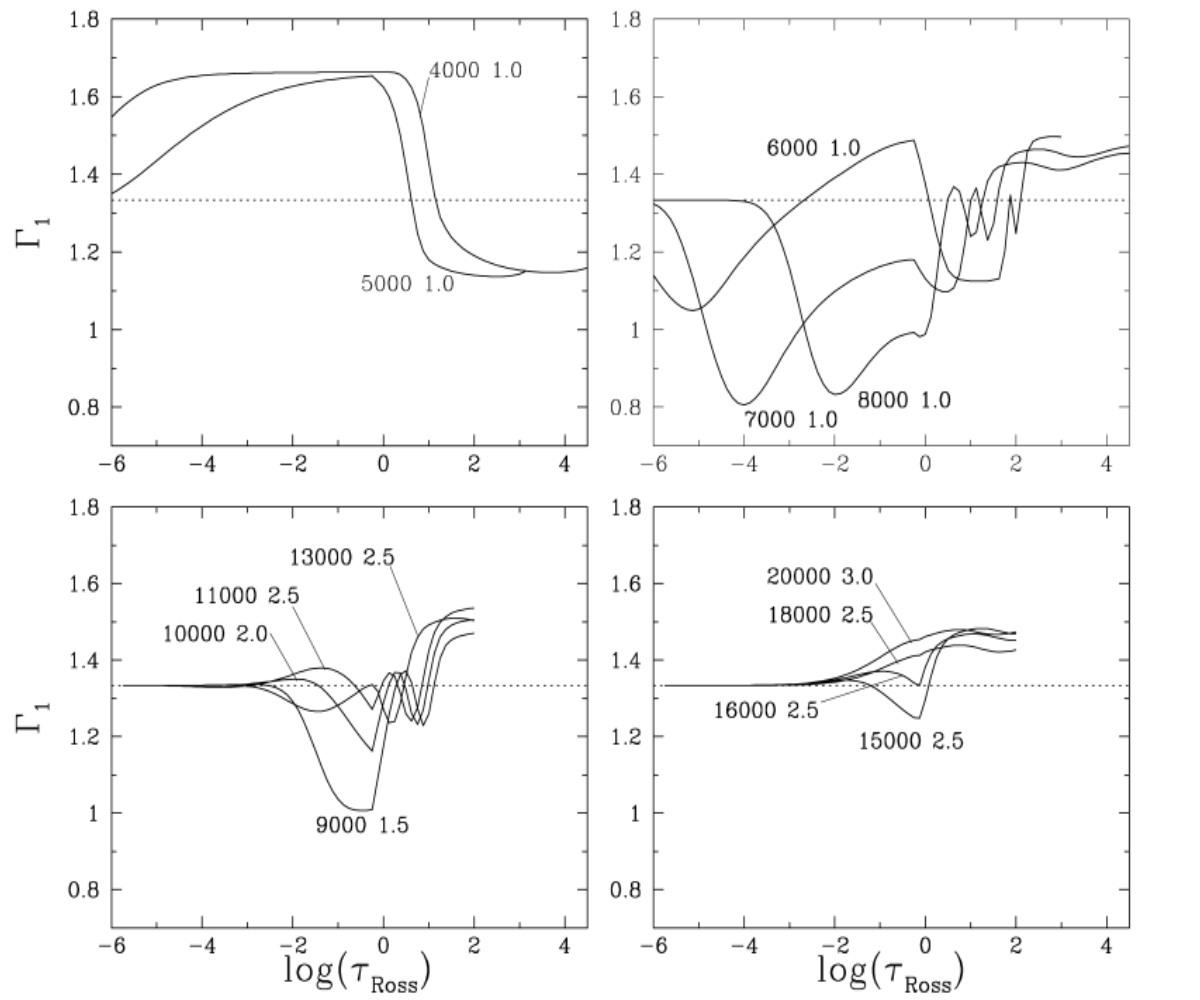
Gamma1 with depth in Teff=8000 K model Gamma1 with depth in model grid
Figure 1: Left-hand panel: The run of Gamma_1 in a model atmosphere with Teff=8000 K and log(g)=1.0. The strong decrease of Gamma_1 to below 4/3 (dotted horizontal line) results from partial non-LTE ionization for optical depths tau_Ross < 2/3 (~R*) (bold solid line). We assume T_rad=Teff and W=1/2 for the computation of Gamma_1 above R*. At larger depths in the photosphere, Gamma_1 mainly decreases due to thermal (LTE) ionization of H and He. The corresponding mean ionization fraction x_bar is shown in the lower panel (bold solid line). At smaller optical depths the gas becomes fully ionized because T_rad exceeds Te. For unrealistic conditions of LTE, with T_rad=Te, these layers would assume a very small x_bar, with larger Gamma_1-values (dash-dotted lines). The influence of the dilution of radiation with distance z above R* is shown with dashed drawn lines. The mean ionization fraction assumes x_bar=0.5 at smaller optical depths when the ionizing radiation field dilutes more with increasing distance z. Consequently, the deep minimum of Gamma_1 in the upper panel, due to partial non-LTE ionization of hydrogen, occurs at smaller optical depths. Right-hand panel: The behavior of Gamma_1 in the outer envelope of supergiants with 4000 K <= Teff <= 20,000 K. Model Teff- and log(g)-values are labeled. The non-LTE Gamma_1 assumes smallest values of ~0.8 above R* (tau_Ross < 2/3) for models with Teff between 7000 K and 8000 K (upper right-hand panel). We assume T_rad=T_eff and W=1/2 for the computation of Gamma_1 above R*. Beneath R*, the LTE Gamma_1-values decrease to below 4/3 (horizontal dotted lines) due to partial ionization of H and He. These thermal ionization zones displace outwards in models with higher Teff, while the partial hydrogen non-LTE ionization region in the outer atmosphere displaces inwards. This causes the deep Gamma_1-minimum for 7000 K <= Teff <= 8000 K. Gamma_1 assumes increasingly larger values for models of higher Teff (lower panels). For models with Teff >= 16,000 K and log(g) >= 2.5 helium is nearly fully ionized, and Gamma_1 assumes values above 4/3 over the entire atmosphere.


Outburst Mechanism of Yellow Supergiants and R CrB Stars

During the 2000-2001 outburst the atmosphere of yellow hypergiant Rho Cas became dynamically unstable because the first generalized adiabatic index < Gamma_1 > volume averaged over the atmosphere assumes values below the stability value of 4/3. < Gamma_1 > < 4/3 when Teff increases above 7250 K during the strong atmospheric collapse before the outburst. The outburst event, directly following this strong collapse, is driven by the release of ionization energy due to the recombination of hydrogen with the cooling of the entire atmosphere by Delta Teff ~= 3500 K. For an adiabatic spherical expansion we calculate that the outburst time-scale is correctly predicted with:

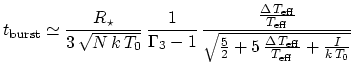
(1)

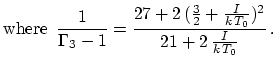
Gamma_3 is the third adiabatic index, evaluated for a mean ionization fraction of 1/2, in the partial hydrogen ionization zone, where the atmosphere is most expandable (or compressible). The run of 1/(Gamma_3 - 1) with T_0 is shown in Fig. 2. For R*=400 R_sun, Teff=7250 K, and T_0 = 8000 K in the partial hydrogen ionization zone with I=13.6 eV, we compute with equation (1) that t_burst=221 d, and an expansion velocity of 36 km/s, which are both in good agreement with the observed values. Hence, we compute that during the outburst of Rho Cas the atmosphere expanded over ~2.5 R* with the complete recombination of hydrogen.

We also estimate that the time-scale over which the total hydrogen recombination energy, released into the circumstellar environment by the outburst, is dissipated by the stellar radiation field during a period following the fast envelope expansion of:

(2)

where sigma is the Stefan-Boltzmann constant. For an atmospheric expansion of d_s = 869 R_sun during the outburst, and a mean envelope density of rho = 10^-10 g/cm^-3 we compute with equation (2) that t_brightness-min ~= 86 d for Teff=3500 K. This time-scale corresponds very well to the period over which the deep brightness minimum of ~100 d was observed in late 2000. The total energy released into the circumstellar environment E_shell = 4 pi R*^2 d_s rho N I with complete hydrogen recombination is ~6.1 10^44 erg. This amount of energy yields a luminosity of L_shell = 1.8 10^4 L_sun, when radiated during 100 d. For a total stellar luminosity of L*= 3.5 10^5 L_sun during quiescent variability phases, L_shell is ~= 5 % of L*.

We compute that during the outburst the partial hydrogen recombination zone of the hypergiant atmosphere dissipates several percent of the stellar luminosity into the stellar environment, thereby driving an expanding wind to highly supersonic outflow velocities during a global cooling of the entire atmosphere by more than 3000 K.

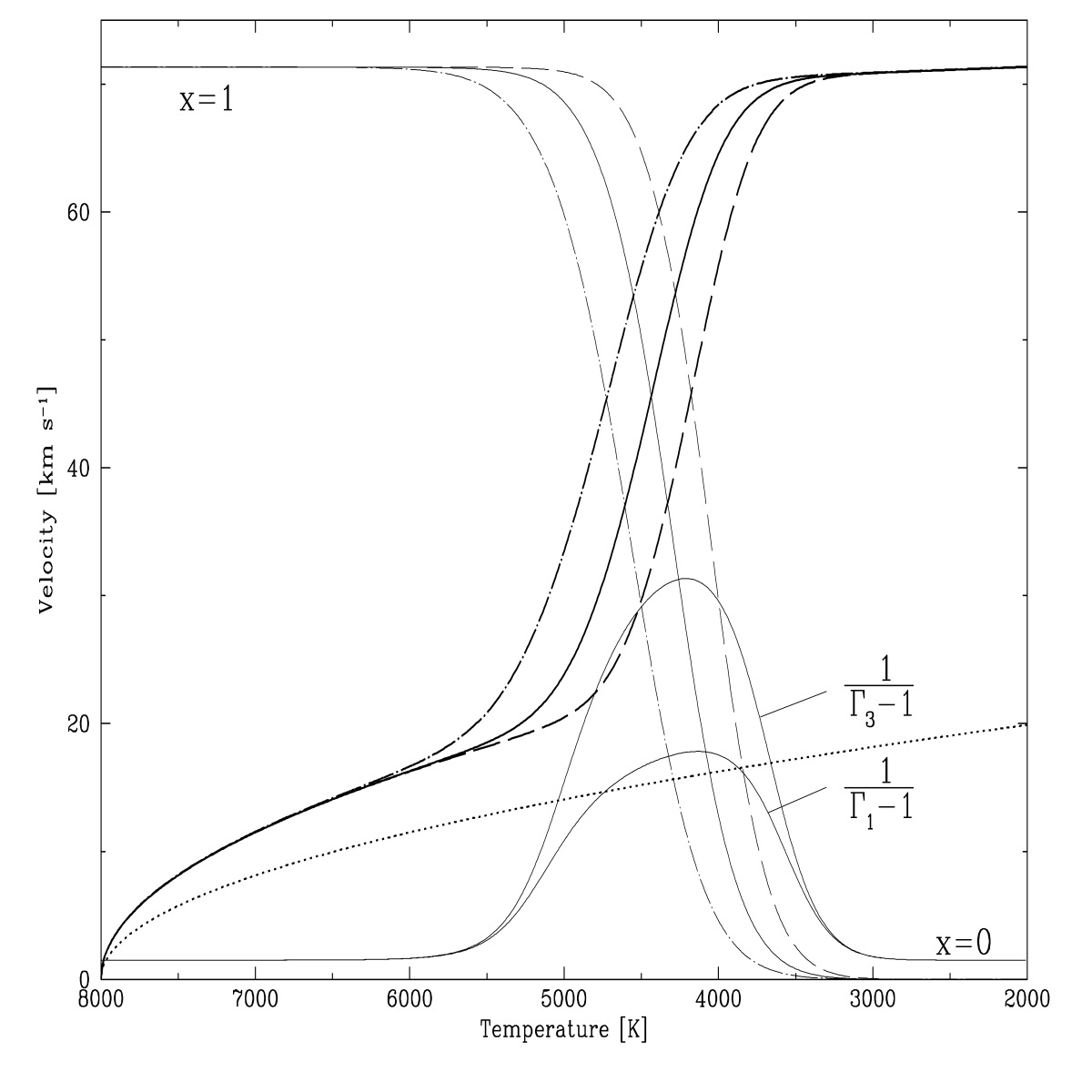
Gamma1 in Rho Cas
Figure 2: The expansion velocity of recombining hydrogen gas with an initial kinetic temperature of 8000 K, computed as a function of the final gas temperature T (boldly drawn lines}). With the recombination during cooling, the velocity of gas parcels that cool to 4000 K <= T <= 6000 K, with an ionization fraction of x~0.5 (thin drawn lines), strongly increases, because the recombination energy drives the expansion with the conservation of total energy and flow momentum. The gas parcels are initially at rest, and their acceleration is computed for flow momenta of 0.1 (dashed drawn lines), 1 (solid lines), and 10 (dash-dotted lines) times the initial gas pressure. In the partial hydrogen ionization-recombination zone the gas parcels become very expandable or compressible, because 1/(Gamma_1 - 1) and 1/(Gamma_3 - 1) assume maximum values. The dotted line is computed without recombination (i.e. pure thermal expansion), which does not yield sufficiently large photospheric expansion velocities observed for the outburst of Rho Cas.


R CrB stars are pulsating supergiants with hydrogen deficient atmospheres. They are smaller and less luminous than the yellow hypergiants, known to also exhibit variability phases that indicate atmospheric outbursts. When these outbursts are driven by the first recombination of helium, equation (1) predicts much shorter outburst time scales. For example, for R CrB, a Ib-supergiant with Teff~=6900 K and R* = 80 R_sun, we compute for T_0=13,000 K in the first helium recombination zone (I_He=24.58 eV) an outburst time of 39 d for Delta Teff=-3500 K. This time scale corresponds to the brightness declines by 3 to 6 magnitudes observed in R CrB-type variables, which occur in less than 50 d. In these smaller stars the outbursts occur faster and more violently than in the yellow hypergiants. The burst-time also depends on the relative abundances of hydrogen and helium, whereas equation (1) assumes a pure hydrogen (or helium) atmosphere. For atmospheric gas mixtures, the last factor of equation (1) requires multi-component expressions for 1/(Gamma_3 - 1), for example computed in Fig. 2 for solar abundance values. In the first ionization zone of helium with T_0=13,000 K, we compute that 1/(Gamma_3 - 1) = 6.67, which yields for Rho Cas t_burst=72 d. This time-scale is at least a factor of two shorter than the observed burst-time, which excludes driving by helium recombination in this luminous cool hypergiant. Note that for Rho Cas we compute that the outburst extends the atmosphere with v=36 km/s over Delta R*= v . t_burst = 988 R_sun (~=2.5 R*), while for R CrB the equation predicts that v=48 km/s and Delta R*=235 R_sun (~=2.9 R*).


Read more: The Upper Luminosity Limit of Massive Stars


Selected Papers